Ohm Solver: Magnetic Reconnection
Hybrid-PIC codes are often used to simulate magnetic reconnection in space plasmas. An example of magnetic reconnection from a force-free sheet is provided, based on the simulation described in Le et al. [10].
Run
The following Python script configures and launches the simulation.
Script PICMI_inputs.py
Listing 41 You can copy this file from
Examples/Tests/ohm_solver_magnetic_reconnection/PICMI_inputs.py.#!/usr/bin/env python3
#
# --- Test script for the kinetic-fluid hybrid model in WarpX wherein ions are
# --- treated as kinetic particles and electrons as an isothermal, inertialess
# --- background fluid. The script demonstrates the use of this model to
# --- simulate magnetic reconnection in a force-free sheet. The setup is based
# --- on the problem described in Le et al. (2016)
# --- https://aip.scitation.org/doi/10.1063/1.4943893.
import argparse
import shutil
import sys
from pathlib import Path
import dill
import numpy as np
from mpi4py import MPI as mpi
from pywarpx import callbacks, fields, libwarpx, picmi
constants = picmi.constants
comm = mpi.COMM_WORLD
simulation = picmi.Simulation(
warpx_serialize_initial_conditions=True,
verbose=0
)
class ForceFreeSheetReconnection(object):
# B0 is chosen with all other quantities scaled by it
B0 = 0.1 # Initial magnetic field strength (T)
# Physical parameters
m_ion = 400.0 # Ion mass (electron masses)
beta_e = 0.1
Bg = 0.3 # times B0 - guiding field
dB = 0.01 # times B0 - initial perturbation to seed reconnection
T_ratio = 5.0 # T_i / T_e
# Domain parameters
LX = 40 # ion skin depths
LZ = 20 # ion skin depths
LT = 50 # ion cyclotron periods
DT = 1e-3 # ion cyclotron periods
# Resolution parameters
NX = 512
NZ = 512
# Starting number of particles per cell
NPPC = 400
# Plasma resistivity - used to dampen the mode excitation
eta = 6e-3 # normalized resistivity
# Number of substeps used to update B
substeps = 20
def __init__(self, test, verbose):
self.test = test
self.verbose = verbose or self.test
# calculate various plasma parameters based on the simulation input
self.get_plasma_quantities()
self.Lx = self.LX * self.l_i
self.Lz = self.LZ * self.l_i
self.dt = self.DT * self.t_ci
# run very low resolution as a CI test
if self.test:
self.total_steps = 20
self.diag_steps = self.total_steps // 5
self.NX = 128
self.NZ = 128
else:
self.total_steps = int(self.LT / self.DT)
self.diag_steps = self.total_steps // 200
# Initial magnetic field
self.Bg *= self.B0
self.dB *= self.B0
self.Bx = (
f"{self.B0}*tanh(z*{1.0/self.l_i})"
f"+{-self.dB*self.Lx/(2.0*self.Lz)}*cos({2.0*np.pi/self.Lx}*x)"
f"*sin({np.pi/self.Lz}*z)"
)
self.By = (
f"sqrt({self.Bg**2 + self.B0**2}-"
f"({self.B0}*tanh(z*{1.0/self.l_i}))**2)"
)
self.Bz = f"{self.dB}*sin({2.0*np.pi/self.Lx}*x)*cos({np.pi/self.Lz}*z)"
self.J0 = self.B0 / constants.mu0 / self.l_i
# dump all the current attributes to a dill pickle file
if comm.rank == 0:
with open(f'sim_parameters.dpkl', 'wb') as f:
dill.dump(self, f)
# print out plasma parameters
if comm.rank == 0:
print(
f"Initializing simulation with input parameters:\n"
f"\tTi = {self.Ti*1e-3:.1f} keV\n"
f"\tn0 = {self.n_plasma:.1e} m^-3\n"
f"\tB0 = {self.B0:.2f} T\n"
f"\tM/m = {self.m_ion:.0f}\n"
)
print(
f"Plasma parameters:\n"
f"\tl_i = {self.l_i:.1e} m\n"
f"\tt_ci = {self.t_ci:.1e} s\n"
f"\tv_ti = {self.vi_th:.1e} m/s\n"
f"\tvA = {self.vA:.1e} m/s\n"
)
print(
f"Numerical parameters:\n"
f"\tdz = {self.Lz/self.NZ:.1e} m\n"
f"\tdt = {self.dt:.1e} s\n"
f"\tdiag steps = {self.diag_steps:d}\n"
f"\ttotal steps = {self.total_steps:d}\n"
)
self.setup_run()
def get_plasma_quantities(self):
"""Calculate various plasma parameters based on the simulation input."""
# Ion mass (kg)
self.M = self.m_ion * constants.m_e
# Cyclotron angular frequency (rad/s) and period (s)
self.w_ce = constants.q_e * abs(self.B0) / constants.m_e
self.w_ci = constants.q_e * abs(self.B0) / self.M
self.t_ci = 2.0 * np.pi / self.w_ci
# Electron plasma frequency: w_pe / omega_ce = 2 is given
self.w_pe = 2.0 * self.w_ce
# calculate plasma density based on electron plasma frequency
self.n_plasma = (
self.w_pe**2 * constants.m_e * constants.ep0 / constants.q_e**2
)
# Ion plasma frequency (Hz)
self.w_pi = np.sqrt(
constants.q_e**2 * self.n_plasma / (self.M * constants.ep0)
)
# Ion skin depth (m)
self.l_i = constants.c / self.w_pi
# # Alfven speed (m/s): vA = B / sqrt(mu0 * n * (M + m)) = c * omega_ci / w_pi
self.vA = abs(self.B0) / np.sqrt(
constants.mu0 * self.n_plasma * (constants.m_e + self.M)
)
# calculate Te based on beta
self.Te = (
self.beta_e * self.B0**2 / (2.0 * constants.mu0 * self.n_plasma)
/ constants.q_e
)
self.Ti = self.Te * self.T_ratio
# calculate thermal speeds
self.ve_th = np.sqrt(self.Te * constants.q_e / constants.m_e)
self.vi_th = np.sqrt(self.Ti * constants.q_e / self.M)
# Ion Larmor radius (m)
self.rho_i = self.vi_th / self.w_ci
# Reference resistivity (Malakit et al.)
self.eta0 = self.l_i * self.vA / (constants.ep0 * constants.c**2)
def setup_run(self):
"""Setup simulation components."""
#######################################################################
# Set geometry and boundary conditions #
#######################################################################
# Create grid
self.grid = picmi.Cartesian2DGrid(
number_of_cells=[self.NX, self.NZ],
lower_bound=[-self.Lx/2.0, -self.Lz/2.0],
upper_bound=[self.Lx/2.0, self.Lz/2.0],
lower_boundary_conditions=['periodic', 'dirichlet'],
upper_boundary_conditions=['periodic', 'dirichlet'],
lower_boundary_conditions_particles=['periodic', 'reflecting'],
upper_boundary_conditions_particles=['periodic', 'reflecting'],
warpx_max_grid_size=self.NZ
)
simulation.time_step_size = self.dt
simulation.max_steps = self.total_steps
simulation.current_deposition_algo = 'direct'
simulation.particle_shape = 1
simulation.use_filter = False
simulation.verbose = self.verbose
#######################################################################
# Field solver and external field #
#######################################################################
self.solver = picmi.HybridPICSolver(
grid=self.grid, gamma=1.0,
Te=self.Te, n0=self.n_plasma, n_floor=0.1*self.n_plasma,
plasma_resistivity=self.eta*self.eta0,
substeps=self.substeps
)
simulation.solver = self.solver
B_ext = picmi.AnalyticInitialField(
Bx_expression=self.Bx,
By_expression=self.By,
Bz_expression=self.Bz
)
simulation.add_applied_field(B_ext)
#######################################################################
# Particle types setup #
#######################################################################
self.ions = picmi.Species(
name='ions', charge='q_e', mass=self.M,
initial_distribution=picmi.UniformDistribution(
density=self.n_plasma,
rms_velocity=[self.vi_th]*3,
)
)
simulation.add_species(
self.ions,
layout=picmi.PseudoRandomLayout(
grid=self.grid,
n_macroparticles_per_cell=self.NPPC
)
)
#######################################################################
# Add diagnostics #
#######################################################################
callbacks.installafterEsolve(self.check_fields)
if self.test:
particle_diag = picmi.ParticleDiagnostic(
name='diag1',
period=self.total_steps,
write_dir='.',
species=[self.ions],
data_list=['ux', 'uy', 'uz', 'x', 'z', 'weighting'],
warpx_file_prefix='Python_ohms_law_solver_magnetic_reconnection_2d_plt',
# warpx_format='openpmd',
# warpx_openpmd_backend='h5',
)
simulation.add_diagnostic(particle_diag)
field_diag = picmi.FieldDiagnostic(
name='diag1',
grid=self.grid,
period=self.total_steps,
data_list=['Bx', 'By', 'Bz', 'Ex', 'Ey', 'Ez'],
write_dir='.',
warpx_file_prefix='Python_ohms_law_solver_magnetic_reconnection_2d_plt',
# warpx_format='openpmd',
# warpx_openpmd_backend='h5',
)
simulation.add_diagnostic(field_diag)
# reduced diagnostics for reconnection rate calculation
# create a 2 l_i box around the X-point on which to measure
# magnetic flux changes
plane = picmi.ReducedDiagnostic(
diag_type="FieldProbe",
name='plane',
period=self.diag_steps,
path='diags/',
extension='dat',
probe_geometry='Plane',
resolution=60,
x_probe=0.0, z_probe=0.0, detector_radius=self.l_i,
target_up_x=0, target_up_z=1.0
)
simulation.add_diagnostic(plane)
#######################################################################
# Initialize #
#######################################################################
if comm.rank == 0:
if Path.exists(Path("diags")):
shutil.rmtree("diags")
Path("diags/fields").mkdir(parents=True, exist_ok=True)
# Initialize inputs and WarpX instance
simulation.initialize_inputs()
simulation.initialize_warpx()
def check_fields(self):
step = simulation.extension.warpx.getistep(lev=0) - 1
if not (step == 1 or step%self.diag_steps == 0):
return
rho = fields.RhoFPWrapper(include_ghosts=False)[:,:]
Jiy = fields.JyFPWrapper(include_ghosts=False)[...] / self.J0
Jy = fields.JyFPAmpereWrapper(include_ghosts=False)[...] / self.J0
Bx = fields.BxFPWrapper(include_ghosts=False)[...] / self.B0
By = fields.ByFPWrapper(include_ghosts=False)[...] / self.B0
Bz = fields.BzFPWrapper(include_ghosts=False)[...] / self.B0
if libwarpx.amr.ParallelDescriptor.MyProc() != 0:
return
# save the fields to file
with open(f"diags/fields/fields_{step:06d}.npz", 'wb') as f:
np.savez(f, rho=rho, Jiy=Jiy, Jy=Jy, Bx=Bx, By=By, Bz=Bz)
##########################
# parse input parameters
##########################
parser = argparse.ArgumentParser()
parser.add_argument(
'-t', '--test', help='toggle whether this script is run as a short CI test',
action='store_true',
)
parser.add_argument(
'-v', '--verbose', help='Verbose output', action='store_true',
)
args, left = parser.parse_known_args()
sys.argv = sys.argv[:1]+left
run = ForceFreeSheetReconnection(test=args.test, verbose=args.verbose)
simulation.step()
Running the full simulation should take about 4 hours if executed on 1 V100 GPU.
For MPI-parallel runs, prefix these lines with
mpiexec -n 4 ... or srun -n 4 ..., depending on the system.
python3 PICMI_inputs.py
Analyze
The following script extracts the reconnection rate as a function of time and animates the evolution of the magnetic field (as shown below).
Script analysis.py
Listing 42 You can copy this file from
Examples/Tests/ohm_solver_magnetic_reconnection/analysis.py.#!/usr/bin/env python3
#
# --- Analysis script for the hybrid-PIC example of magnetic reconnection.
import glob
import dill
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors
plt.rcParams.update({'font.size': 20})
# load simulation parameters
with open(f'sim_parameters.dpkl', 'rb') as f:
sim = dill.load(f)
x_idx = 2
z_idx = 4
Ey_idx = 6
Bx_idx = 8
plane_data = np.loadtxt(f'diags/plane.dat', skiprows=1)
steps = np.unique(plane_data[:,0])
num_steps = len(steps)
num_cells = plane_data.shape[0]//num_steps
plane_data = plane_data.reshape((num_steps, num_cells, plane_data.shape[1]))
times = plane_data[:, 0, 1]
dt = np.mean(np.diff(times))
plt.plot(
times / sim.t_ci,
np.mean(plane_data[:,:,Ey_idx], axis=1) / (sim.vA * sim.B0),
'o-'
)
plt.grid()
plt.xlabel(r'$t/\tau_{c,i}$')
plt.ylabel('$<E_y>/v_AB_0$')
plt.title("Reconnection rate")
plt.tight_layout()
plt.savefig("diags/reconnection_rate.png")
if not sim.test:
from matplotlib.animation import FFMpegWriter, FuncAnimation
from scipy import interpolate
# Animate the magnetic reconnection
fig, axes = plt.subplots(3, 1, sharex=True, figsize=(7, 9))
for ax in axes.flatten():
ax.set_aspect('equal')
ax.set_ylabel('$z/l_i$')
axes[2].set_xlabel('$x/l_i$')
datafiles = sorted(glob.glob("diags/fields/*.npz"))
num_steps = len(datafiles)
data0 = np.load(datafiles[0])
sX = axes[0].imshow(
data0['Jy'].T, origin='lower',
norm=colors.TwoSlopeNorm(vmin=-0.6, vcenter=0., vmax=1.6),
extent=[0, sim.LX, -sim.LZ/2, sim.LZ/2],
cmap=plt.cm.RdYlBu_r
)
# axes[0].set_ylim(-5, 5)
cb = plt.colorbar(sX, ax=axes[0], label='$J_y/J_0$')
cb.ax.set_yscale('linear')
cb.ax.set_yticks([-0.5, 0.0, 0.75, 1.5])
sY = axes[1].imshow(
data0['By'].T, origin='lower', extent=[0, sim.LX, -sim.LZ/2, sim.LZ/2],
cmap=plt.cm.plasma
)
# axes[1].set_ylim(-5, 5)
cb = plt.colorbar(sY, ax=axes[1], label='$B_y/B_0$')
cb.ax.set_yscale('linear')
sZ = axes[2].imshow(
data0['Bz'].T, origin='lower', extent=[0, sim.LX, -sim.LZ/2, sim.LZ/2],
# norm=colors.TwoSlopeNorm(vmin=-0.02, vcenter=0., vmax=0.02),
cmap=plt.cm.RdBu
)
cb = plt.colorbar(sZ, ax=axes[2], label='$B_z/B_0$')
cb.ax.set_yscale('linear')
# plot field lines
x_grid = np.linspace(0, sim.LX, data0['Bx'][:-1].shape[0])
z_grid = np.linspace(-sim.LZ/2.0, sim.LZ/2.0, data0['Bx'].shape[1])
n_lines = 10
start_x = np.zeros(n_lines)
start_x[:n_lines//2] = sim.LX
start_z = np.linspace(-sim.LZ/2.0*0.9, sim.LZ/2.0*0.9, n_lines)
step_size = 1.0 / 100.0
def get_field_lines(Bx, Bz):
field_line_coords = []
Bx_interp = interpolate.interp2d(x_grid, z_grid, Bx[:-1].T)
Bz_interp = interpolate.interp2d(x_grid, z_grid, Bz[:,:-1].T)
for kk, z in enumerate(start_z):
path_x = [start_x[kk]]
path_z = [z]
ii = 0
while ii < 10000:
ii+=1
Bx = Bx_interp(path_x[-1], path_z[-1])[0]
Bz = Bz_interp(path_x[-1], path_z[-1])[0]
# print(path_x[-1], path_z[-1], Bx, Bz)
# normalize and scale
B_mag = np.sqrt(Bx**2 + Bz**2)
if B_mag == 0:
break
dx = Bx / B_mag * step_size
dz = Bz / B_mag * step_size
x_new = path_x[-1] + dx
z_new = path_z[-1] + dz
if np.isnan(x_new) or x_new <= 0 or x_new > sim.LX or abs(z_new) > sim.LZ/2:
break
path_x.append(x_new)
path_z.append(z_new)
field_line_coords.append([path_x, path_z])
return field_line_coords
field_lines = []
for path in get_field_lines(data0['Bx'], data0['Bz']):
path_x = path[0]
path_z = path[1]
l, = axes[2].plot(path_x, path_z, '--', color='k')
# draws arrows on the field lines
# if path_x[10] > path_x[0]:
axes[2].arrow(
path_x[50], path_z[50],
path_x[250]-path_x[50], path_z[250]-path_z[50],
shape='full', length_includes_head=True, lw=0, head_width=1.0,
color='g'
)
field_lines.append(l)
def animate(i):
data = np.load(datafiles[i])
sX.set_array(data['Jy'].T)
sY.set_array(data['By'].T)
sZ.set_array(data['Bz'].T)
sZ.set_clim(-np.max(abs(data['Bz'])), np.max(abs(data['Bz'])))
for ii, path in enumerate(get_field_lines(data['Bx'], data['Bz'])):
path_x = path[0]
path_z = path[1]
field_lines[ii].set_data(path_x, path_z)
anim = FuncAnimation(
fig, animate, frames=num_steps-1, repeat=True
)
writervideo = FFMpegWriter(fps=14)
anim.save('diags/mag_reconnection.mp4', writer=writervideo)
if sim.test:
import os
import sys
sys.path.insert(1, '../../../../warpx/Regression/Checksum/')
import checksumAPI
# this will be the name of the plot file
fn = sys.argv[1]
test_name = os.path.split(os.getcwd())[1]
checksumAPI.evaluate_checksum(test_name, fn)
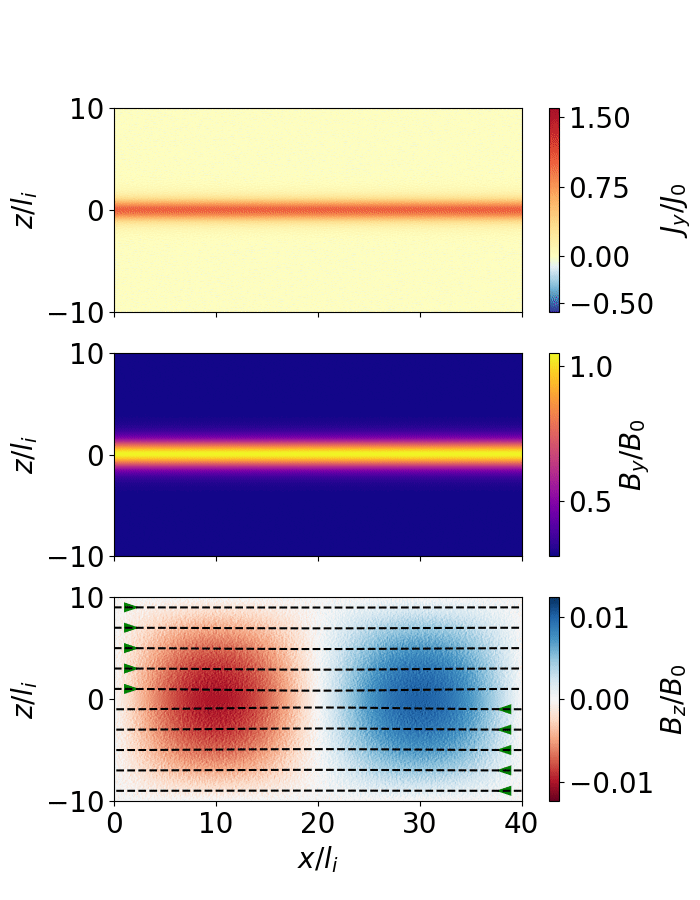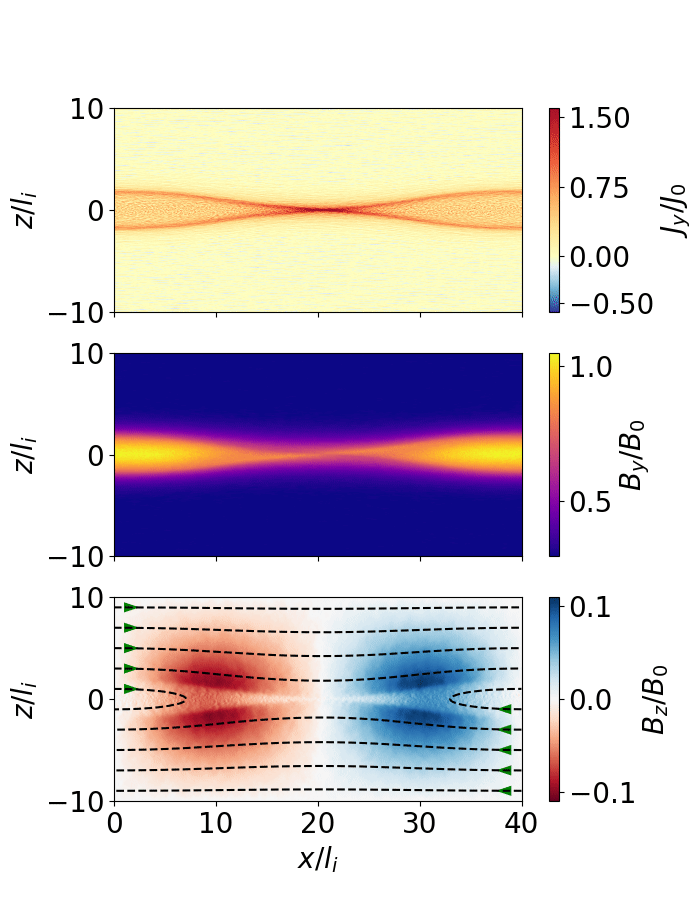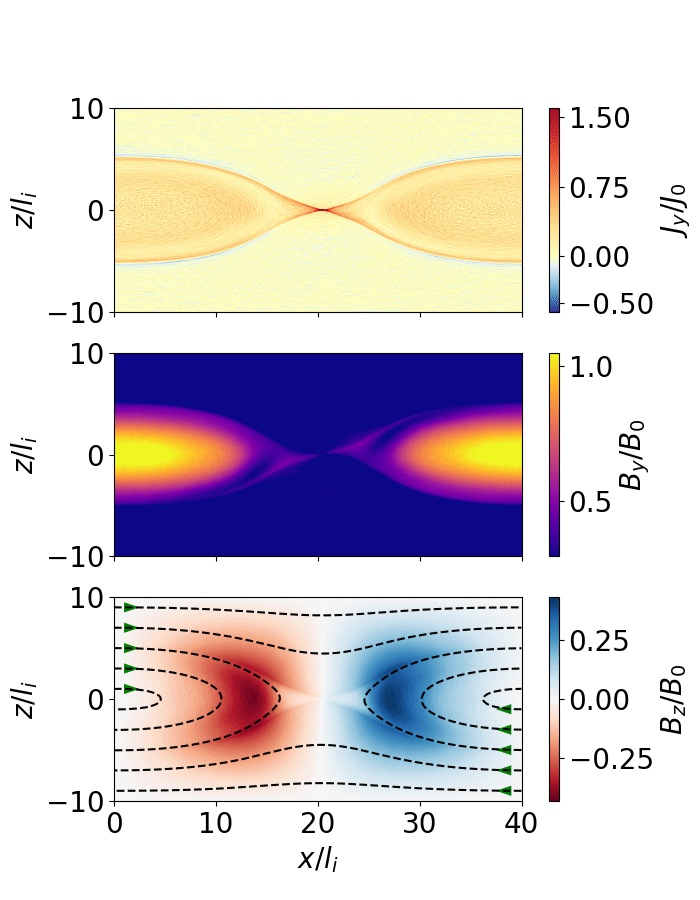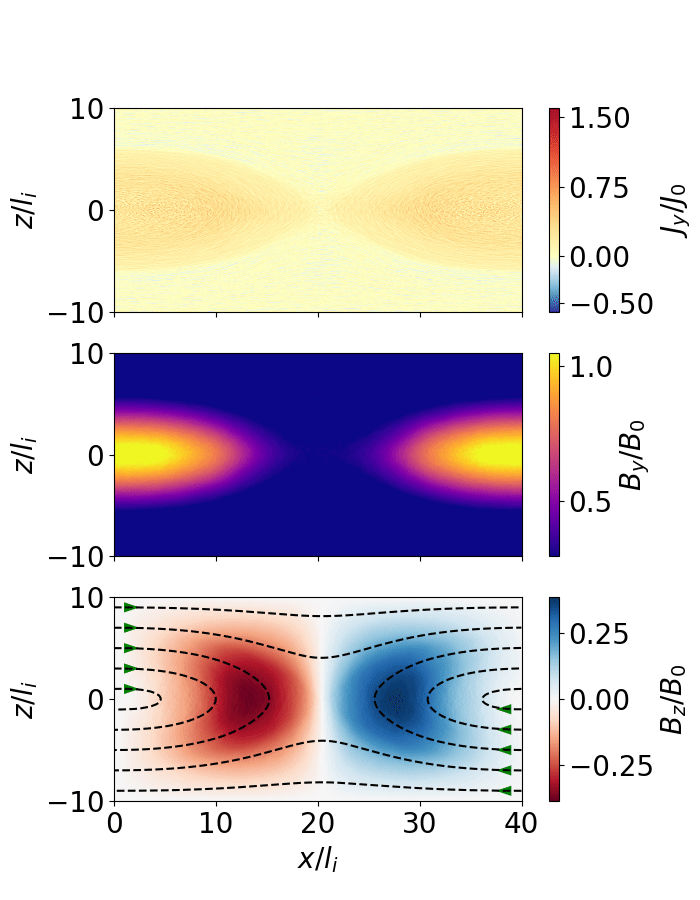
Fig. 7 Magnetic reconnection from a force-free sheet.