Introduction
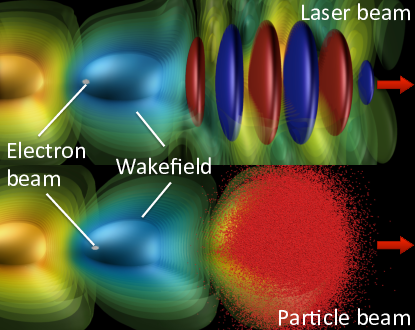
Fig. 26 Plasma laser-driven (top) and charged-particles-driven (bottom) acceleration (rendering from 3-D Particle-In-Cell simulations). A laser beam (red and blue disks in top picture) or a charged particle beam (red dots in bottom picture) propagating (from left to right) through an under-dense plasma (not represented) displaces electrons, creating a plasma wakefield that supports very high electric fields (pale blue and yellow). These electric fields, which can be orders of magnitude larger than with conventional techniques, can be used to accelerate a short charged particle beam (white) to high-energy over a very short distance.
Computer simulations have had a profound impact on the design and understanding of past and present plasma acceleration experiments [1, 2, 3, 4, 5]. Accurate modeling of wake formation, electron self-trapping and acceleration require fully kinetic methods (usually Particle-In-Cell) using large computational resources due to the wide range of space and time scales involved. Numerical modeling complements and guides the design and analysis of advanced accelerators, and can reduce development costs significantly. Despite the major recent experimental successes [6, 7, 8, 9], the various advanced acceleration concepts need significant progress to fulfill their potential. To this end, large-scale simulations will continue to be a key component toward reaching a detailed understanding of the complex interrelated physics phenomena at play.
For such simulations, the most popular algorithm is the Particle-In-Cell (or PIC) technique, which represents electromagnetic fields on a grid and particles by a sample of macroparticles. However, these simulations are extremely computationally intensive, due to the need to resolve the evolution of a driver (laser or particle beam) and an accelerated beam into a structure that is orders of magnitude longer and wider than the accelerated beam. Various techniques or reduced models have been developed to allow multidimensional simulations at manageable computational costs: quasistatic approximation [10, 11, 12, 13, 14], ponderomotive guiding center (PGC) models [11, 12, 14, 15, 16], simulation in an optimal Lorentz boosted frame [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29], expanding the fields into a truncated series of azimuthal modes [30, 31, 32, 33, 34], fluid approximation [12, 15, 35] and scaled parameters [4, 36].
F. S. Tsung, W. Lu, M. Tzoufras, W. B. Mori, C. Joshi, J. M. Vieira, L. O. Silva, and R. A. Fonseca. Simulation Of Monoenergetic Electron Generation Via Laser Wakefield Accelerators For 5-25 TW Lasers. Physics of Plasmas, 13(5):56708, May 2006. doi:10.1063/1.2198535.
C. G. R. Geddes, D. L. Bruhwiler, J. R. Cary, W. B. Mori, J.-L. Vay, S. F. Martins, T. Katsouleas, E. Cormier-Michel, W. M. Fawley, C. Huang, X. Wang, B. Cowan, V. K. Decyk, E. Esarey, R. A. Fonseca, W. Lu, P. Messmer, P. Mullowney, K. Nakamura, K. Paul, G. R. Plateau, C. B. Schroeder, L. O. Silva, C. Toth, F. S. Tsung, M. Tzoufras, T. Antonsen, J. Vieira, and W. P. Leemans. Computational Studies And Optimization Of Wakefield Accelerators. In Journal of Physics: Conference Series, volume 125, 012002 (11 Pp.). 2008.
C. G.R. Geddes, E. Cormier-Michel, E. H. Esarey, C. B. Schroeder, J.-L. Vay, W. P. Leemans, D. L. Bruhwiler, J. R. Cary, B. Cowan, M. Durant, P. Hamill, P. Messmer, P. Mullowney, C. Nieter, K. Paul, S. Shasharina, S. Veitzer, G. Weber, O. Rubel, D. Ushizima, W. Bethel, and J. Wu. Laser Plasma Particle Accelerators: Large Fields For Smaller Facility Sources. In Scidac Review 13, number 13, 13–21. 2009. URL: https://www.osti.gov/biblio/971264.
C. G. R. Geddes, E. Cormier-Michel, E. Esarey, C. B. Schroeder, and W. P. Leemans. Scaled Simulation Design Of High Quality Laser Wakefield Accelerator Stages. In Proc. Particle Accelerator Conference. Vancouver, Canada, 2009.
C. Huang, W. An, V. K. Decyk, W. Lu, W. B. Mori, F. S. Tsung, M. Tzoufras, S. Morshed, T. Antonsen, B. Feng, T. Katsouleas, R. A. Fonseca, S. F. Martins, J. Vieira, L. O. Silva, E. Esarey, C. G. R. Geddes, W. P. Leemans, E. Cormier-Michel, J.-L. Vay, D. L. Bruhwiler, B. Cowan, J. R. Cary, and K. Paul. Recent Results And Future Challenges For Large Scale Particle-In-Cell Simulations Of Plasma-Based Accelerator Concepts. Journal of Physics: Conference Series, 180(1):012005 (11 Pp.), 2009.
W. P. Leemans, A. J. Gonsalves, H.-S. Mao, K. Nakamura, C. Benedetti, C. B. Schroeder, Cs. Tóth, J. Daniels, D. E. Mittelberger, S. S. Bulanov, J.-L. Vay, C. G. R. Geddes, and E. Esarey. Multi-GeV Electron Beams from Capillary-Discharge-Guided Subpetawatt Laser Pulses in the Self-Trapping Regime. Phys. Rev. Lett., 113(24):245002, Dec 2014. URL: http://link.aps.org/doi/10.1103/PhysRevLett.113.245002, doi:10.1103/PhysRevLett.113.245002.
I. Blumenfeld, C. E. Clayton, F.-J. Decker, M. J. Hogan, C. Huang, R. Ischebeck, R. Iverson, C. Joshi, T. Katsouleas, N. Kirby, W. Lu, K. A. Marsh, W. B. Mori, P. Muggli, E. Oz, R. H. Siemann, D. Walz, and M. Zhou. Energy doubling of 42[thinsp]GeV electrons in a metre-scale plasma wakefield accelerator. Nature, 445(7129):741–744, Feb 2007. URL: http://dx.doi.org/10.1038/nature05538.
S. V. Bulanov, J. J. Wilkens, T. Z. Esirkepov, G. Korn, G. Kraft, S. D. Kraft, M. Molls, and V. S. Khoroshkov. Laser ion acceleration for hadron therapy. Physics-Uspekhi, 57(12):1149, 2014. URL: http://stacks.iop.org/1063-7869/57/i=12/a=1149.
S. Steinke, J. van Tilborg, C. Benedetti, C. G. R. Geddes, C. B. Schroeder, J. Daniels, K. K. Swanson, A. J. Gonsalves, K. Nakamura, N. H. Matlis, B. H. Shaw, E. Esarey, and W. P. Leemans. Multistage coupling of independent laser-plasma accelerators. Nature, 530(7589):190–193, Feb 2016. URL: http://dx.doi.org/10.1038/nature16525 http://10.1038/nature16525.
P. Sprangle, E. Esarey, and A. Ting. Nonlinear theory of intense laser-plasma interactions. Physical Review Letters, 64(17):2011–2014, Apr 1990.
T. M. Antonsen and P. Mora. Self-Focusing And Raman-Scattering Of Laser-Pulses In Tenuous Plasmas. Physical Review Letters, 69(15):2204–2207, Oct 1992. doi:10.1103/Physrevlett.69.2204.
J. Krall, A. Ting, E. Esarey, and P. Sprangle. Enhanced Acceleration In A Self-Modulated-Laser Wake-Field Accelerator. Physical Review E, 48(3):2157–2161, Sep 1993. doi:10.1103/Physreve.48.2157.
P. Mora and T. M. Antonsen. Kinetic Modeling Of Intense, Short Laser Pulses Propagating In Tenuous Plasmas. Phys. Plasmas, 4(1):217–229, Jan 1997. doi:10.1063/1.872134.
C. Huang, V. K. Decyk, C. Ren, M. Zhou, W. Lu, W. B. Mori, J. H. Cooley, T. M. Antonsen, Jr, and T. Katsouleas. Quickpic: A Highly Efficient Particle-In-Cell Code For Modeling Wakefield Acceleration In Plasmas. Journal of Computational Physics, 217(2):658–679, Sep 2006. doi:10.1016/J.Jcp.2006.01.039.
C. Benedetti, C. B. Schroeder, E. Esarey, C. G. R. Geddes, and W. P. Leemans. Efficient Modeling Of Laser-Plasma Accelerators With Inf&Rno. Aip Conference Proceedings, 1299:250–255, 2010. doi:10.1063/1.3520323.
B. M. Cowan, D. L. Bruhwiler, E. Cormier-Michel, E. Esarey, C. G. R. Geddes, P. Messmer, and K. M. Paul. Characteristics Of An Envelope Model For Laser-Plasma Accelerator Simulation. Journal of Computational Physics, 230(1):61–86, 2011. doi:Doi: 10.1016/J.Jcp.2010.09.009.
J.-L. Vay. Noninvariance Of Space- And Time-Scale Ranges Under A Lorentz Transformation And The Implications For The Study Of Relativistic Interactions. Physical Review Letters, 98(13):130405/1–4, 2007.
D. L. Bruhwiler, J. R. Cary, B. M. Cowan, K. Paul, C. G. R. Geddes, P. J. Mullowney, P. Messmer, E. Esarey, E. Cormier-Michel, W. Leemans, and J.-L. Vay. New Developments In The Simulation Of Advanced Accelerator Concepts. In Aip Conference Proceedings, volume 1086, 29–37. 2009.
J.-L. Vay, D. L. Bruhwiler, C. G. R. Geddes, W. M. Fawley, S. F. Martins, J. R. Cary, E. Cormier-Michel, B. Cowan, R. A. Fonseca, M. A. Furman, W. Lu, W. B. Mori, and L. O. Silva. Simulating Relativistic Beam And Plasma Systems Using An Optimal Boosted Frame. Journal of Physics: Conference Series, 180(1):012006 (5 Pp.), 2009.
J.-L. Vay, W. M. Fawley, C. G. R. Geddes, E. Cormier-Michel, and D. P. Grote. Application of the reduction of scale range in a Lorentz boosted frame to the numerical simulation of particle acceleration devices. In Proc. Particle Accelerator Conference. Vancouver, Canada, 2009.
S. F. Martins, R. A. Fonseca, L. O. Silva, and W. B. Mori. Boosted Frame PIC Simulations of LWFA: Towards the Energy Frontier. In Proc. Particle Accelerator Conference. Vancouver, Canada, 2009.
J.‐L. Vay, C. G. R. Geddes, C. Benedetti, D. L. Bruhwiler, E. Cormier‐Michel, B. M. Cowan, J. R. Cary, and D. P. Grote. Modeling Laser Wakefield Accelerators In A Lorentz Boosted Frame. AIP Conference Proceedings, 1299(1):244–249, Nov 2010. URL: https://doi.org/10.1063/1.3520322, arXiv:https://pubs.aip.org/aip/acp/article-pdf/1299/1/244/11928106/244\_1\_online.pdf, doi:10.1063/1.3520322.
S. F. Martins, R. A. Fonseca, W. Lu, W. B. Mori, and L. O. Silva. Exploring Laser-Wakefield-Accelerator Regimes For Near-Term Lasers Using Particle-In-Cell Simulation In Lorentz-Boosted Frames. Nature Physics, 6(4):311–316, Apr 2010. doi:10.1038/Nphys1538.
S. F. Martins, R. A. Fonseca, J. Vieira, L. O. Silva, W. Lu, and W. B. Mori. Modeling Laser Wakefield Accelerator Experiments With Ultrafast Particle-In-Cell Simulations In Boosted Frames. Physics of Plasmas, 17(5):56705, May 2010. doi:10.1063/1.3358139.
S. F. Martins, R. A. Fonseca, L. O. Silva, W. Lu, and W. B. Mori. Numerical Simulations Of Laser Wakefield Accelerators In Optimal Lorentz Frames. Computer Physics Communications, 181(5):869–875, May 2010. doi:10.1016/J.Cpc.2009.12.023.
J.-L. Vay, C. G. R. Geddes, E. Cormier-Michel, and D. P. Grote. Numerical Methods For Instability Mitigation In The Modeling Of Laser Wakefield Accelerators In A Lorentz-Boosted Frame. Journal of Computational Physics, 230(15):5908–5929, Jul 2011. doi:10.1016/J.Jcp.2011.04.003.
J.-L. Vay, C. G. R. Geddes, E. Cormier-Michel, and D. P. Grote. Effects of hyperbolic rotation in Minkowski space on the modeling of plasma accelerators in a Lorentz boosted frame. Physics of Plasmas, 18(3):030701, Mar 2011. URL: https://doi.org/10.1063/1.3559483, arXiv:https://pubs.aip.org/aip/pop/article-pdf/doi/10.1063/1.3559483/16019930/030701\_1\_online.pdf, doi:10.1063/1.3559483.
J.-L. Vay, C. G. R. Geddes, E. Esarey, C. B. Schroeder, W. P. Leemans, E. Cormier-Michel, and D. P. Grote. Modeling Of 10 GeV-1 TeV Laser-Plasma Accelerators Using Lorentz Boosted Simulations. Physics of Plasmas, Dec 2011. doi:10.1063/1.3663841.
P. Yu, X. Xu, A. Davidson, A. Tableman, T. Dalichaouch, F. Li, M. D. Meyers, W. An, F. S. Tsung, V. K. Decyk, F. Fiuza, J. Vieira, R. A. Fonseca, W. Lu, L. O. Silva, and W. B. Mori. Enabling Lorentz boosted frame particle-in-cell simulations of laser wakefield acceleration in quasi-3D geometry. Journal of Computational Physics, 2016. doi:10.1016/j.jcp.2016.04.014.
B. B. Godfrey. The IPROP Three-Dimensional Beam Propagation Code. Defense Technical Information Center, 1985.
A. F. Lifschitz, X. Davoine, E. Lefebvre, J. Faure, C. Rechatin, and V. Malka. Particle-in-Cell modelling of laser-plasma interaction using Fourier decomposition. Journal of Computational Physics, 228(5):1803–1814, 2009. URL: http://www.sciencedirect.com/science/article/pii/S0021999108005950, doi:http://dx.doi.org/10.1016/j.jcp.2008.11.017.
A. Davidson, A. Tableman, W. An, F. S. Tsung, W. Lu, J. Vieira, R. A. Fonseca, L. O. Silva, and W. B. Mori. Implementation of a hybrid particle code with a PIC description in r–z and a gridless description in \Phi into OSIRIS. Journal of Computational Physics, 281:1063–1077, 2015. doi:10.1016/j.jcp.2014.10.064.
R. Lehe, M. Kirchen, I. A. Andriyash, B. B. Godfrey, and J.-L. Vay. A spectral, quasi-cylindrical and dispersion-free Particle-In-Cell algorithm. Computer Physics Communications, 203:66–82, 2016. doi:10.1016/j.cpc.2016.02.007.
I. A. Andriyash, R. Lehe, and A. Lifschitz. Laser-plasma interactions with a Fourier-Bessel particle-in-cell method. Physics of Plasmas, 23(3):, 2016. doi:10.1063/1.4943281.
B. A. Shadwick, C. B. Schroeder, and E. Esarey. Nonlinear Laser Energy Depletion In Laser-Plasma Accelerators. Physics of Plasmas, 16(5):56704, May 2009. doi:10.1063/1.3124185.
E. Cormier-Michel, C. G. R. Geddes, E. Esarey, C. B. Schroeder, D. L. Bruhwiler, K. Paul, B. Cowan, and W. P. Leemans. Scaled Simulations Of A 10 GeV Accelerator. In Aip Conference Proceedings, volume 1086, 297–302. 2009.